第四届线性解法器算法与性能优化竞赛

关于SolverChallenge

        SolverChallenge竞赛是解法器快速算法及应用研讨会（SOLVER会议）的一项特色活动，由SOLVER会议组委会主办，每年举行一次。竞赛针对实际应用中抽取出来的线性代数问题，要求参赛队伍在一定约束条件下通过算法设计与性能调优等手段对这些系统进行数值求解，并基于不同标准从多个维度对所获结果进行评价。第四届竞赛（SolverChallenge24）将与第七届解法器快速算法及应用研讨会（SOLVER24，四川成都）同期启动，欢迎解法器领域的同行及研究生报名参赛。

竞赛背景

       
        线性代数方程组 Ax=b 是科学与工程计算领域面临的共性问题，求解该类方程的解法器已成为很多应用软件的性能瓶颈。当前，国产高性能计算机已进入百亿亿次（E级）计算时代。这些国际领先的超级计算机为我国科学与工程计算应用迈进超大规模计算时代、实现更高精细的数值模拟成为可能。然而，超大规模计算给解法器算法设计与性能优化带来巨大挑战。一方面，超大规模计算必然是求解越来越复杂的实际应用问题，更加精细的物理建模蕴含着越来越复杂的应用特征（如：多时空尺度、多物理耦合、多介质、复杂流动、强非线性强间断、长时间积分等），从而导致现有解法器算法的计算复杂度急剧增长。另一方面，随着计算机硬件性能的提升，超级计算机呈现“多级嵌套海量并行、异构众核加速”的复杂体系结构特征，导致解法器算法的实现效率急剧下降。这种“应用与机器”的双重复杂性导致解法器越来越成为实际数值模拟应用的性能瓶颈，如何设计能同时匹配实际应用特征和机器体系结构特征的快速算法与性能优化技术是当前亟待解决的关键问题。

        

竞赛宗旨

       
        SolverChallenge竞赛瞄准我国重要行业应用中的解法器瓶颈问题，赛题源于实际应用的需求，并根据每年的需求和优化情况持续更新。一方面，希望通过检验参赛队伍的算法与软件对这些问题的适应性，从中筛选出合适的算法及解法器策略，为应用提供新的思路与解决途径，提升我国重要行业应用中自主软件的解法器计算能力。另一方面，希望通过实际问题的牵引，吸引更多科研人员开展应用驱动的解法器算法创新与性能优化研究，同时培养具有交叉学科背景的优秀青年研究人员和研究生。

        

竞赛方案与规则

竞赛方案

       
        竞赛组委会提供10套来源于不同应用领域的线性系统（每套线性系统包括矩阵A和右端向量b、存储格式的描述、求解约束条件等），参赛选手针对这10套系统进行求解，不限制求解方法（即迭代法、直接法或混合方法均可），也不限制解法器软件包的来源。竞赛网站将提供程序中输入、输出与计时部分，并开放接口供参赛选手提交自己的执行代码（若是闭源的，则提交链接文件）。最终将使用不同的右端向量b测试，其求解效果（速度、精度、浮点运算次数等）将作为本竞赛奖项评判标准。

竞赛规则

       
        硬件环境：竞赛指定硬件作为程序性能的测试平台，参赛选手有权使用竞赛测试平台，但使用时间将被限制，在使用时间内参赛选手可以配置环境与测试程序。在竞赛提供的平台测出的成绩会作为参赛选手的最终成绩。

        指定硬件包括：

        1. 商用 CPU（Intel Xeon Platinum 8358, 2 路共 64 核，频率 2.6 GHz, 内存 256 GB DDR4）;
        2. 商用 CPU（Intel Xeon Platinum 8468V, 2 路共 96 核，频率 2.4 GHz, 内存 1536 GB DDR4）+ GPU（NVIDIA H20，4096 CUDA 核，频率 2.4 GHz，显存 96 GB HBM3，8 卡）;
        3. 国产 CPU（Huawei Kunpeng 920-6426，2 路共 128 核，频率 2.6 GHz，内存 512GB DDR4）+ 商用 GPU（NVIDIA A100，6912 CUDA 核，频率 1.4 GHz，显存 40 GB HBM2，1 卡）;

        本次比赛提供的超算环境仅限使用单个节点。

        软件环境：准许使用任何软件包参与竞赛，但是在评分时会考虑所使用软件包的自主性和创新性。

        参赛队伍：竞赛面向本科生与研究生开放，学生采用自愿组合方式组成参赛队伍。每支队伍人数不超过3人，且应指定1-2名指导教师。

文档内容规范

       
        算法设计实现涉及到的技术栈：包含采用的硬件、系统环境、软件；
        算法详细内容：包含采用的算法、参数；
        总体思路：包含问题的简要分析、求解策略；
        结果分析（注明使用内存的情况）；
        遇到的问题。

评分依据

       
        求解速度（到解墙上时间）：评分标准同时考虑求解的线性系统个数与性能。每个系统满分10分，能正确解出且性能最优者得满分，其他选手的成绩依次顺延，未能解出者不得分。所有10组系统得分累加得到总成绩。此外，为让各队伍积极参与，鼓励大家设计创新的思路，只要保证能解出正确结果，会给予基准分。
        评分公式：在赛题不特殊说明下，分数 =（Tmin/Tself）* (10 - x) + x，其中 Tmin 为正确解出赛题的所有参赛队伍中用时最少的时间，Tself 为参赛队伍的时间，x 为基准分（默认基准分为1分）。
        例如：求解某一系统时，假设基准分为x=1，排名第一的参赛小组用时120ms、排名第二的参赛小组用时240ms、排名第三的参赛小组用时800ms、排名第四的参赛小组用时10000ms甚至更多，排名第五的参赛小组未解出，则第一参赛小组得10分，第二参赛小组得5.5分，第三参赛小组得2.35分，第四参赛小组得1.108分，第五参赛小组得0分。

        限制：确保求解出的解向量x满足相应的精度要求，每道题限制使用单节点计算资源。

        

奖项设定

       
        竞赛专委会将根据参赛作品的创新性、完成度、文档质量、难度以及答辩表现等情况进行评奖。

        基础奖项：按照求解速度与浮点运算次数得分，分别设特等奖（不超1名），一等奖（不超过15%）、二等奖（不超过30%）、三等奖若干；
        特别奖项：创新奖（在算法或性能优化方法方面有独特创新）、单系统奖（对于某一个线性系统有独特贡献）等；
        企业特别奖：赞助厂商可根据自己的需求评选企业特别奖。

        

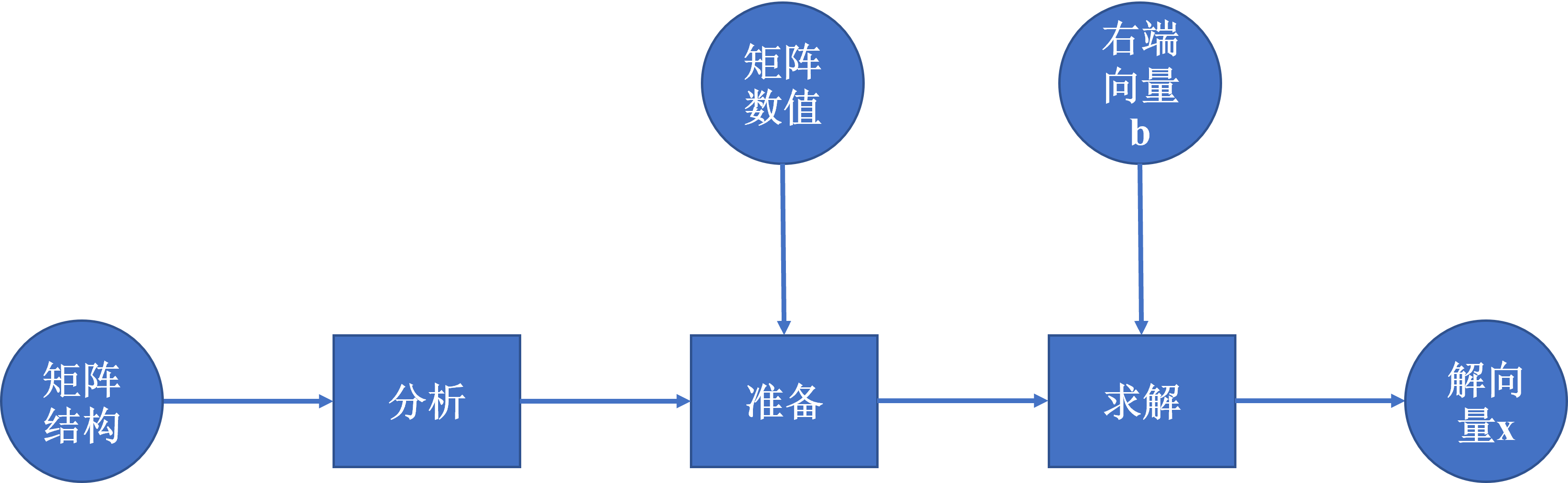
竞赛流程

事项 时间
开启报名 6月3日
公布赛题
 6月3日
报名截止
 6月20日
开启程序提交
 6月20日
关闭程序提交
 7月8日
初评、公布入围名单
 7月15日
在SOLVER24会议上进行答辩、颁奖
 7月22日-7月26日

竞赛截止报名时间

       
        2024 年 6 月 20 日

竞赛报名方式

       
竞赛报名请点击此处填写表格，或扫描下方二维码



        

第四届解法器算法及优化竞赛（SolverChallenge24）赛题

百度网盘：下载链接   提取码:  qhxp

赛题说明

端到端时间可分为如下3部分:
1. 分析
2. 准备
3. 求解
矩阵和向量的读入、格式转换、分发至多进程、矩阵坐标排序不列入统计时间。

直接法和迭代法对于上述3步的定义略有不同。

直接法：
1. 分析：利用矩阵结构信息（即不依赖矩阵数值），做解法器预处理，包括图分析、图优化、预开辟空间、节点优化编号等操作，参考intel pardiso的phase=11（注意，pardiso phase=11可以传入矩阵的值做一定的处理，本次比赛不允许）。
2. 准备：利用矩阵数值信息做数值分解，参考intel pardiso phase=22。
3. 求解：输入右端向量b，得到解向量x，参考intel pardiso phase=33。

迭代法：
1. 分析：利用矩阵结构信息（即不依赖矩阵数值），做解法器预处理，包括预条件子构建、多重网格构建等。
2. 准备：利用矩阵数值信息做数值准备，包括预条件子数值准备，多重网格数值准备等。
3. 求解：输入右端向量b，得到解向量x。

注： 若将直接法作为预条件子用在迭代法中，则直接法部分参考“直接法”的说明计入迭代法三项相应时间中。

1、不同题目对于时间的要求不同，请选手注意。
2、关于矩阵说明，今年所有题目统一成1-base矩阵（矩阵中非零元素索引从1开始）。
3、组委会提供的三个硬件环境均已下载所有赛题，参赛选手请勿重复下载。
4、关于赛题的参考代码，请参见：SolverChallenge24_sample_code。

赛题名称 solverchallenge24_01
矩阵阶数 9,104,256
非零元数 272,717,760
应用领域 激光聚变
来源与背景描述   PDE：激光聚变黑腔与靶丸耦合辐射能量传输模拟，三维多群辐射输运方程；
网格类型：非结构网格；
离散格式：角度：离散纵标法（方向数24），空间：迎风格式。
MD5 e4fa6428d66a8f731226aee014c99240
约束 ||r||2 / ||b||2 < 1e-12;
内存要求：无。
关注时间
 端到端时间
分数说明 基准分为1分，满分为10分
赛题名称 solverchallenge24_02
矩阵阶数 19,637,808
非零元数 97,535,322  
应用领域 复杂流动
来源与背景描述   PDE：航空发动机燃烧室仿真三维压力方程；
网格类型：非结构网格；
离散格式：单元中心有限体积。
MD5 e5f4ee8e14799cc5e6e55ee80e9819e2
约束 （1）||r||2 / ||b||2 < 1e-6;
（2）||r||2 / ||b||2 < 1e-10;
内存要求：无。
关注时间
 端到端时间
分数说明 达到约束(1)：基准分为1分，满分为5分；
达到约束(2)：基准分为1分，满分为5分；
约束(1)和约束(2)分别计分，总分为两者累加。
赛题名称 solverchallenge24_03
矩阵阶数 2,081,541
非零元数 71,033,481
应用领域 结构力学
来源与背景描述   PDE：航空发动机整机静力学仿真，接触力学线弹性方程；
离散格式：一阶节点有限元，每个节点定义三个自由（位移三个分量）；
网格类型：非结构网格；
特点：带有复杂约束条件。
MD5 b32e5c5a873e45efd1474ea32530089d
约束 ||r||2 / ||b||2 < 1e-8;
内存要求：无。
关注时间
 端到端时间
分数说明 基准分为1分，满分为10分
赛题名称 solverchallenge24_04
矩阵阶数 12,582,822
非零元数 678,943,908
应用领域 结构力学
来源与背景描述   PDE：三维线弹性方程；
网格类型：非结构网格；
网格规模：非结构网格;
离散格式：有限元。   
MD5 fa9287eed458d36b7b4a3b8440ac58eb
约束 ||r||2 / ||b||2 < 1e-8;
内存要求：无;
初始x0为零向量。
关注时间
 端到端时间
分数说明 基准分为1分，满分为10分
赛题名称 solverchallenge24_05
矩阵阶数 4,951,702
非零元数 612,096,612
应用领域 生物医疗
来源与背景描述   PDE：三维流体-相场-刚体耦合方程；
网格类型：非结构四面体网格；
网格规模：618,962网格点；
离散格式：P1-P1压力稳定化，带刚体约束条件。
MD5 db60668e876e10d52c7c5146bab59853
约束 ||r||2 / ||b||2 < 1e-10;
内存要求：无。
关注时间
 端到端时间
分数说明 基准分为1分，满分为10分
赛题名称 solverchallenge24_06
矩阵阶数 1,765,074
非零元数 28,533,594
应用领域 电子学系统
来源与背景描述   PDE：滤波器电磁场仿真时谐麦克斯韦方程；
离散格式：一阶Nedelec有限元，每条边一个自由度；
特点：离散矩阵为复型系统。
MD5 3c6e4ea6fc406269feb0960a1ebd4493
约束 ||r||2 / ||b||2 < 1e-8;
内存要求：无;
初始x0为零向量。
关注时间
 端到端时间
分数说明 基准分为1分，满分为10分
赛题名称 solverchallenge24_07
矩阵阶数 34,421,777
非零元数 244,364,753
应用领域 集成电路
来源与背景描述   EMIR仿真；
矩阵非常稀疏，是一个M-matrix。
MD5 0a1f5b494c0c4ce8e138a06f36ed8495
约束 ||r||2 / ||b||2 < 1e-12
提示
 该题是固定矩阵多右端项的问题，数据中提供了时间步上连续的三个右端项，它们之间有一定的关联性，可以利用上一时间步的解加速当前时间步的求解。
关注时间
 三套系统的端到端时间
分数说明 基准分为1分，满分为10分
赛题名称 solverchallenge24_08
矩阵阶数 5,809,680
非零元数 194,348,610
应用领域 集成电路
来源与背景描述   电路谐波平衡分析;
电路工艺：T65；
特点：离散矩阵为复型系统。
MD5 bbfc342f135e0453efd0655f01251839
约束 ||r||2 / ||b||2 < 1e-8;
内存要求：无。
提示
 请认真分析矩阵元素结构和数值分布，多为块矩阵；可以考虑迭代法，预处理子一般选为将每个块矩阵变成对角矩阵（或三对角、五对角等），或变成更小的对角块矩阵；也可以考虑直接法，注意填入元个数。该题块大小15x15，块类型：满阵/对角阵。
关注时间
 准备+求解
分数说明 基准分为1分，满分为10分
赛题名称 solverchallenge24_09
矩阵阶数 9,683,038
非零元数 75,425,210  
应用领域 集成电路
来源与背景描述   集成电路瞬态仿真方程；
电路类型：sram后仿电路；
电路工艺：16nm。
MD5 846efc9ae6a3e4457f9815c522f9a3cc
约束 ||r||2 / ||b||2 < 1e-8；
内存要求：100G以下。
提示
 一般用直接法
关注时间
 准备+求解
分数说明 基准分为1分，满分为10分
赛题名称 solverchallenge24_10
矩阵阶数 418,718
非零元数 921,708,586
应用领域 集成电路
来源与背景描述   射频电路谐波平衡仿真方程；
电路类型：VCO；
电路工艺：28nm；
特点：离散矩阵为复型系统。
MD5 0ba7f3ada999bdb196a1df72e5a5c68d
约束 ||r||2 / ||b||2 < 1e-8;
内存要求：无。
提示
 请认真分析矩阵元素结构和数值分布，多为块矩阵；可以考虑迭代法，预处理子一般选为将每个块矩阵变成对角矩阵（或三对角、五对角等），或变成更小的对角块矩阵；也可以考虑直接法，注意填入元个数。
关注时间
 准备+求解
分数说明 基准分为1分，满分为10分

竞赛组织

       
        主办单位：解法器快速算法及应用研讨会组织委员会
        承办单位：电子科技大学

        

竞赛评奖委员会共同主席

        徐小文（北京应用物理与计算数学研究所）
        张晨松（中国科学院数学与系统科学研究院）
        舒    适（湘潭大学）
        谭光明（中国科学院计算技术研究所）
        刘伟峰（中国石油大学（北京））
        薛    巍（清华大学、青海大学）

竞赛评奖委员会委员

        安恒斌（北京应用物理与计算数学研究所）
        崔    涛（中国科学院数学与系统科学研究院）
        冯春生（湘潭大学）
        荆燕飞（电子科技大学）
        刘伟峰（中国石油大学（北京））
        舒    适（湘潭大学）
        谭光明（中国科学院计算技术研究所）
        王欣亮（华为技术有限公司）
        谢和虎（中国科学院数学与系统科学研究院）
        徐小文（北京应用物理与计算数学研究所）
        薛    巍（清华大学、青海大学）
        张晨松（中国科学院数学与系统科学研究院）
        周振亚（北京华大九天科技股份有限公司）

竞赛联系人

       
        赵    梨： 18373287736 (电话) | lizhao@lsec.cc.ac.cn (邮箱)
        毛润彰： 19310195829 (电话) | mrz@nudt.edu.cn (邮箱)